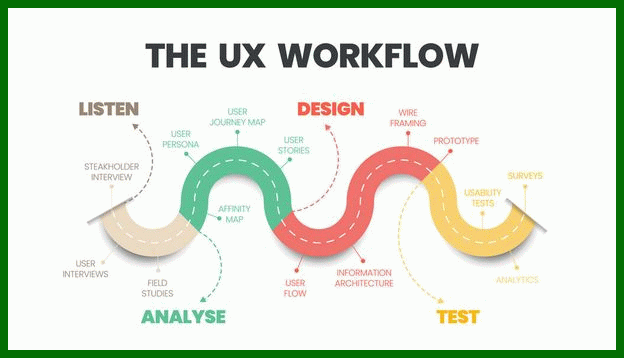
21 امتیاز برای یک وب سایت خبری کاربردی و مخاطب پسند
- پیمایش آسان: منوی منظم و دستهبندیهای واضح به کاربران کمک میکند تا اخبار مورد علاقه خود را به سرعت پیدا کنند.
- طراحی واکنشگرا: وبسایت باید برای دستگاههای مختلف، از جمله رایانههای رومیزی، تبلتها و تلفنهای هوشمند بهینهسازی شود تا از تجربه کاربری یکپارچه اطمینان حاصل شود.
- سرعت بارگذاری سریع: زمان بارگذاری سریع صفحه برای تعامل و حفظ کاربر بسیار مهم است.
- نوشتن واضح و مختصر: مقالات خبری باید به زبانی ساده و قابل فهم و با تمرکز بر دقت و عینیت نوشته شوند.
- اخبار بهروز: محتوای بهروز شده منظم، کاربران را در جریان و درگیر نگه میدارد.
- فرمتهای محتوای چندگانه: فرمتهای محتوای مختلف، مانند متن، تصاویر، ویدئوها و اینفوگرافیکها را برای پاسخگویی به تنظیمات برگزیده کاربران مختلف ترکیب کنید.
- عملکرد جستجو: یک نوار جستجو به کاربران امکان می دهد مقالات یا موضوعات خاص خبری را به راحتی پیدا کنند.
- رابط کاربر پسند: یک طرحبندی تمیز و بدون درهمریختگی با عناوین، زیرعنوانها و اندازههای فونت واضح، خوانایی و قابلیت استفاده را افزایش میدهد.
- بخش نظرات: اجازه دادن به نظرات کاربر باعث تعامل و بحث میشود، اما اعتدال برای حفظ یک محیط مدنی و مرتبط ضروری است.
- منابع موثق: برای حفظ اعتبار وب سایت از نظر دقت و قابل اعتماد بودن، منابع معتبر را ذکر کنید.
- محتوای محلی: شامل اخبار مرتبط با موقعیت جغرافیایی مخاطب هدف برای افزایش ارتباط و تعامل.
- شخصیسازی: توصیههای محتوای سفارشیشده را بر اساس علایق کاربران و سابقه مرور ارائه دهید.
- ادغام رسانههای اجتماعی: دکمههای اشتراکگذاری و فیدهای رسانههای اجتماعی کاربران را تشویق میکند تا محتوا را به اشتراک بگذارند و وبسایت را در پلتفرمهای دلخواه خود دنبال کنند.
- خبرنامههای ایمیل: خبرنامههای معمولی، کاربران را از آخرین اخبار مطلع میکند و باعث افزایش ترافیک به وبسایت میشود.
- برنامه تلفن همراه: یک برنامه تلفن همراه اختصاصی یک پلت فرم اختصاصی برای دسترسی به اخبار در حال حرکت در اختیار کاربران قرار می دهد.
- پشتیبانی چند زبانه: ارائه محتوا به زبانهای مختلف، مخاطبان بیشتری را تامین میکند و دسترسی جهانی را افزایش میدهد.
- دسترسپذیری: اطمینان حاصل کنید که وبسایت از دستورالعملهای دسترسی به وب پیروی میکند و آن را برای کاربران دارای معلولیت در دسترس قرار میدهد.
- امنیت: برای محافظت از دادههای کاربر و حفظ اعتماد، رمزگذاری SSL و سایر اقدامات امنیتی را اجرا کنید.
- مدیریت تبلیغات: با محدود کردن تبلیغات مزاحم و اطمینان از عدم تداخل در مصرف محتوا، درآمد تبلیغات را با تجربه کاربر متعادل کنید.
- شفافیت: خطمشیهای سرمقاله، مالکیت، و اطلاعات تماس وبسایت را بهروشنی نمایش دهید تا اعتماد و مسئولیتپذیری را ارتقا دهید.
- تعامل کاربر: به طور منظم با کاربران از طریق نظرسنجی، نظرسنجی و سایر ویژگیهای تعاملی تعامل داشته باشید تا اولویتهای آنها را درک کنید و وبسایت را بهبود ببخشید.
چه چیزی یک وب سایت خبری محبوب را می سازد
- محتوای مرتبط و بهموقع: یک وبسایت خبری پرطرفدار بهطور مداوم محتوایی را ارائه میکند که با مخاطب هدف خود مرتبط است و اخبار فوری را در صورت وقوع پوشش میدهد.
- اعتماد: شهرت قوی برای دقت، انصاف و بی طرفی برای ایجاد و حفظ خوانندگان وفادار بسیار مهم است.
- محتوای جذاب: ترکیبی از محتوای آموزنده، تحقیقی و سرگرم کننده، کاربران را درگیر میکند و برای اطلاعات بیشتر بازمیگردند.
- طراحی کاربر محور: وبسایتی که به راحتی قابل پیمایش است، از نظر بصری جذاب است و برای دستگاههای مختلف بهینه شده است، تجربه کاربری مثبتی را تضمین میکند.
- حضور در رسانههای اجتماعی: حضور فعال و جذاب در پلتفرمهای رسانههای اجتماعی به گسترش دامنه دسترسی وبسایت کمک میکند و حس اجتماعی را در میان کاربران تقویت میکند.
- ویژگی های نوآورانه: ترکیب ویژگی های منحصر به فرد، مانند واقعیت مجازی یا واقعیت افزوده، می تواند یک وب سایت خبری را از رقبا متمایز کند و کاربران جدید را جذب کند.
- هویت برند قوی: هویت برند متمایز، شامل لوگوی به یاد ماندنی و زبان بصری ثابت، به وبسایت کمک میکند در بازار شلوغ برجسته شود.
- تمرکز محلی: پوشش اخبار و رویدادهای محلی، علاوه بر داستانهای ملی و بینالمللی، به ایجاد ارتباط با مخاطبان و تقویت آن کمک میکند.حس اجتماع دارد.
- روزنامه نگاران خبره: بکارگیری روزنامه نگاران با تجربه، آگاه و مورد احترام به اعتبار وب سایت کمک می کند و خوانندگان وفادار را جذب می کند.
- تعامل: تشویق به مشارکت کاربر از طریق نظرات، انجمنها و سایر ویژگیهای تعاملی، حس اجتماعی و تعامل را تقویت میکند.
- اطلاعات آماری مبتنی بر داده: استفاده از تجزیه و تحلیل دادهها برای درک رفتار و اولویتهای کاربر به وبسایت اجازه میدهد تا محتوای خود را تنظیم کند و تجربه کاربر را بهبود بخشد.
- مدلهای درآمد نوآورانه: بررسی جریانهای درآمدی جایگزین، مانند مدلهای اشتراک یا محتوای حمایتشده، میتواند به وبسایت خبری کمک کند استقلال خود را حفظ کند و از تکیه صرف به تبلیغات اجتناب کند.
- دسترسی جهانی: گسترش دامنه دسترسی وبسایت با ارائه محتوا به زبانهای مختلف و ارائه خدمات به مخاطبان متنوع میتواند منجر به افزایش محبوبیت و درآمد شود.
- همکاریهای اینفلوئنسر: مشارکت با افراد یا سازمانهای با نفوذ میتواند به ارتقای وبسایت و جذب کاربران جدید کمک کند.
- بهبود مستمر: بهروزرسانی و اصلاح منظم وبسایت بر اساس بازخورد کاربر و روند صنعت، تضمین میکند که رقابتی و مرتبط باقی بماند
گزیده ای از عناوین سایت خبری آسمونی
جدیدترین اخبار ایرج طهماسب
نقد و بررسی فیلم کلاشینکف
تنها چیزی که خانومها از زندگی میخوان !!!
مرغ باربیکیو؛ غذایی لذیذ برای مهمانی ها یا مسافرت
عکس پروفایل زمستانی؛ مخصوص دخترها
جدیدترین روش کاشت مو با کمترین دوره نقاهت و مزایا و معایب
معمای سخت انیشتین به همراه پاسخ آن
درباره بسیج دانش آموزی بدانید
آشنایی با زندگی ماهی فایتر
جان در تن بیجان (نگاهى به دو فیلم چهلمین جشنواره فیلم فجر)
اطلاعاتی در مورد دستگاه های بدنسازی
مشاوره کسب و کار؛ جانی دوباره به کسب و کار خود
بک لینک چیست؟ چگونه بک لینک معتبر بسازیم؟
معرفی شهرستان بانه + تاریخچه و عکس
چرا بیش از 8000 امام زاده در ایران وجود دارد ؟
پنج مدل موی بسیار شیک و آسان
چرا زنها رهبر ارکستر نمیشوند؟
پیش شماره تلفن های ثابت زنجان
سرویس های هوشمند IN مخابرات منطقه تهران
اوقات فراغت خود را چگونه پر کنیم ؟
مدالهای المپیک در گذر زمان
بهترین فروشگاه های فرش و تابلوفرش؛ آدرس وشماره تماس
باورهای دینی ایرانیان در زمان هخامنشی
شاید زنده بمانم – قسمت ششم
سکه پارسیان؛ قیمت و نکات خرید
بهترین رستورانهای ژاپنی در تهران؛ آدرس
آشنایی با گوشی آنر Magic5 Ultimate
عوامل آلودگی هوا عبارتند از …
ضمایر موصولی در زبان انگلیسی
قیمت گوشت حیوانات و آبزیان؛ آذر ۱۴۰۲
فواید و مزایای فعالیت بدنی و ورزش
شبها به این خوراکیها نه بگویید
طنز؛ به علت باران جشنواره کن لغو شد
دیالوگ های ماندگار تاریخ سینما
کاربرد بیوتکنولوژی در صنعت نساجی
2 نکته طلایی برای افزایش سلامت باتری آیفون
غرفه سازی در تهران؛ طراحی، ساخت، نصب غرفه نمایشگاهی
یک نکته طلایی برای زندگی مشترک
توکیو و داستان تکراری میزبانی المپیک
فیلم سینمایی توتسی به کارگردانی سیدنی پولاک
فیلم سارا و آیدا، درامی از مازیار میری
نقد روان شناختی فیلم سینمایی تیرانازوروس
گاوبازی ورزشی مهیج و بسیار خطرناک
زندگینامه آیت الله میرزا حسن شیرازی
محصولات آنتی ایجینگ و ضد پیری
نگاهى به مجموعه جیران، از قصه تا واقعیت
طرح های مختلف تاتو فارسی و انگلیسی
آیا برای عضله سازی باید استراحت کرد؟
آموزش دسته گل با کلم چینی
اجاره کالا و لوازم؛ روشی برای درآمدزایی
طرح جینف (استانداردسازی آدرس پستی) چیست و چه مزایایی دارد؟
اوتمیل چیست؟ طرز تهیه چند صبحانه خوشمزه با اوت میل
تیمهایی که حاضر به شرکت در جام جهانی نشدند
بیوگرافی شکیرا؛ خواننده کلمبیایی و همسر سابق پیکه
آموزش چیدمان صحیح مبلمان در خانه
بیوگرافی سجاد شهباززاده؛ مهاجم گلزن استقلال تهران
در شب یلدا چه اتفاقاتی رخ می دهد؟
سرمربی 75 میلیارد تومانی و ده مخالف سرشناس!
پوشیدن جوراب سفید برای آقایان ممنوع!
آشنایی با دانشگاه آکسفورد
اعلام داروهای غیرمجاز و ممنوعه برای حجاج
بلیط تایلند؛ شرایط سفر به تایلند
نمودار قیمت چیست؟ از نمودار قیمت سکه تا دلار
سریال غریبه هایی از جهنم؛ عدم اعتماد همانند بازی مرکب
28 رجب ؛ حرکت امام حسین علیه السلام از مدینه به مکه
تاریخچه پیدایش جشن عید نوروز
آشنایی با استان اصفهان؛ جاهای دیدنی
شورای امنیت سازمان ملل متحد
راز عجیب یک ماهی بنفش در اعماق دریا
معرفی مراکز خرید غرب تهران، گشت و گذاری در بهترین های پایتخ
15نشانه سرطان که زنان نادیده میگیرند
ورزش پارکور ، هنر جابجایی
بهبود روابط جنسی با رژیم غذایی مناسب
عجیب ترین نوع اعتراض به داوری در مسابقات ورزشی
دیدار فوتبالی روی برف با بازیکنان پالتوپوش
سریال فراتر از بهشت؛ اسپینآف سریال جنایت در بهشت
اصول و فروع دین اسلام به ترتیب چیست؟
یه دوست پسر هم نداریم که …
زندگینامه کیان ایرانی، کیان ابوعمره کیسان
بارش برف و باران امروز در بسیاری از نقاط کشور
بهترین هتل های خارجی معروف در دنیا
تصاویری زیبا از شمع آرایی
بهترین موسسات خدمات حسابداری، مالی و مالیاتی
انیمه، مانگا، مانهوا، وبتون و کمیک؛ تفاوت آنها چیست؟
بهترین فروشگاه تجهیزات ورزشی در تهران
مفهوم پسورد یا گذرواژه؛ نکات مهم در انتخاب یک رمز مناسب
بهترین ساعت برای دویدن و لاغر شدن
نیمار و افشای راز دوستی بزرگش با مسی
بهترین راه برطرف کردن درد زانو
بیوگرافی رعنا آزادی ور: بازیگر سریال زخم کاری
نگاهى به فیلم ابجى، یک فیلم دوست داشتنى
طرز تهیه سوپ قارچ؛ غذایی مفید در هوای سرد پاییز
سریال آقای آفتاب؛ سریال تاریخی و نقش زنان در استقلال کره
به مناسبت سالروز تولد محمدعلی کلی، بزرگ ترین بوکسور تاریخ
متن های خاص عاشقانه و زیبای تبریک تولد مادر
آموزشگاه های گویندگی و دوبلاژ در تهران
افزایش طول عمر با گیاه جنسینگ
با قطار به مشهد برویم یا اتوبوس و یا هواپیما ؟
هک کردن و معرفی دو هکر مشهور
همگرایی و همسویی کشورها و ادیان
قاتل حضرت ابولفضل چه کسی بود
نقاشی های بی نظیر از Susan Rios
سنجدهای سفره هفتسین را بخورید؛ فواید بیشمار سنجد
معمای (پنج) کلاه و (سه) نفر
قیمت گوشت حیوانات و آبزیان؛ آذر ۱۴۰۲
چند داستان جالب و خواندنی از ایران باستان
دیوار صوتی چیست و چگونه شکسته می شود؟
هایلی هایسر ؛ زنی که در لیگ حرفه ای مردان گلزنی کرد
آموزش ساخت صندلی فانتزی با قوطی نوشابه
انواع زنبور، از عسل و گاوی تا قرمز و قاتل !
طرز تهیه موهیتو؛ نوشیدنی پرطرفدار هوای گرم تابستانی
نمایشگاه سوغات، کالا و جهیزیه ایرانی
۸ اسفند، روز امور تربیتی و تربیت اسلامی
دروازه بانی با رکورد عجیب 2 گل خورده در هشت سال!
سیاست مدار ایرانی در آمریکا
تاثیر و خواص رنگ قرمز و آبی
لحظه ای با جمله های زندگی
تزیین خیار و خیار شور به شکل گل رز
آشنایی با روش تهیه ته چین قیسی
با بدن تان به صحبت های همسر خود گوش دهید
نقد فیلم عروسی مردم، فیلم یا تبلیغ براى سالن عروسی
عکس هایی از گل ها و گیاهان در کرج
چرا بعضی وقتها حس میکنیم بچه ها با دوستانشان بهترخوش هستند
طرز تهیه کورن داگ یا سوسیس چوبی
اگر مدام خسته اید بخوانید
چه کسانی در انتخابات ریاست جمهوری 1400 ثبت نام کردند؟
۲۸ صفر؛ رحلت رسول اکرم صلی الله علیه و اله و سلم
اتوبوس چیست ، تاریخچه + انواع اتوبوس های مسافربری
بیوگرافی رونالدو نازاریو؛ ال فنومنو، مرد تاریخی فوت
نمایشگاه بین المللی کتاب تهران ۱۴۰۱
بهترین آرایشگاه های کرج؛ آدرس و شماره تماس
خود مراقبتی؛ خود مراقبتی را بشناسید
بهترین فیلم های کارگردانی شده که هفت اسکار دارد
قلعه کنگلو سوادکوه مازندران، عقاب مازندران
تاریخ و زمان حرکت پیاده روی اربعین
آرایش مخصوص شب یلدا، با تم هندوانه و انار
راز زیبایی موهای زنان هندی چیست؟
پایگاه های خبری معروف خارجی
راهنمای انتخاب هتل و راهنمای رزرو هتل
پیست های معروف در کشورهای مختلف کدامند؟
تیمی آلمانی با دو هوادار!
شرایط و هزینه زندگی در کره جنوبی
باغ راه فدک تهران، محبوب ترین پارک پایتخت
بهترین مرکز فروش تجهیزات پزشکی و مهندسی پزشکی در تهران
آشنایی با لوگوی تیمهای فوتبالی ؛ بلکبرن
هرمس کهن الگوی مردانه؛ خدای تغییروتحول،نوجوان ابدی
برف از کجا می آید و نماد چیست؟
راه اندازی کسب و کار با سرمایه کم
پیام تبریک ولادت امام سجاد (ع)
بهترین ماسکهای صورت برای از بین بردن لکههای تیره
مقاصد پرمشتری گردشگری در اروپا
معرفی برنامه های جایگزین اسنپ چت
تعریف بانک به زبان ساده و انواع بانک
عکس از صدف های زیبای دریایی
نوشیدنی هایی که شما را آرام میکند
در این روز ماه سبز رنگ خواهد شد
مدرسه فیضیه قم (مدرسه شیخ نوری)
مراقب امتحان کیست و چه وظیفه خطیری دارد؟
معرفی زبان برنامه نویسی ارلنگ
بلیط سیستمی هواپیما چیست؟
آشنایی با علائم کم آبی بدن
کارت های پیش پرداخت؛ معرفی کارت های PrePaid
20 خرداد؛ شهادت آیت الله سعیدی به دست ماموران ستم شاهی (13
طرز تهیه چای خوش عطر آلبالو
نقد فیلم جوان روس ، برنده جایزه بهترین فیلم در بخش سینمای ج
7 می ، روز جهانی کتاب کمیک رایگان
روش تشخیص سکه های اصل از تقلبی
انرژی هسته ای چگونه تولید می شود؟
مدلینگ در شمال؛ موقعیت های استان های شمالی برای مدل شدن
بازیکنان سپاهان و اتوبان یکطرفه به سمت پرسپولیس
بهترین فروشندگان سیستم های صوتی
وزنه برداری که 161 بار رکوردشکنی کرد!
متعصب ترین تماشاگر آرسنال و مرگ پدر
سخنان زیبای مرحوم حسین پناهی
چند مدل تونیک تابستانه برای خانم ها
طرز تهیه فرنی مجلسی برای افطار
مرکز پژوهشهای مجلس شورای اسلامی ایران
بهترین سریالهای کرهای سال ۲۰۲۳
بیوگرافی کیانوش رستمی؛ قهرمان المپیک ریو 2016
اولین دوپینگی ورزش دنیا که بود؟
پن کیک موز؛ عصرانهای لذیذ و خوشمزه
خواهران پرس و مشکوک ترین رکوردهای جهانی
روانشناسی واقعیت گرایی و واقعیت درمانی
اَللّهمَ صَلّ عَلی مُحَمَّد وَ آلِ محمد ، (صلوات) کلید درب بهشت
اسامی و القاب پیامبران و امامان
چرا ماه رمضان به عید ختم می شود؟
صنعت مد و پوشاک ایرانی اسلامی
آش اسفناج آش سرماخوردگی؛ طرز تهیه
بیوگرافی محمدرضا گلزار؛ سوپر استار ایران
5 خرداد، اکتشاف نفت نخستین بار در تاریخ ایران در مسجد سلیم
نقد و معرفی سریال حیثیت گمشده
حدیث های کوتاه از پیامبر (ص)
آشنایی با شهرستان ورامین تهران
راهنمای خرید مبل تختخواب شو
مراقبت از طبیعت ، شاید شانس آخر ما برای نجات خانه مان باشد!
معرفی تیمهای حاضر در جام ملت های آسیا
نقد فیلم حافظه، سرگرم کننده اما بى محتوا
منطقه 51 و رازهای مربوط به آن چیست؟
تبریک تولد خودمونی و پیام دوستانه تولد
5 خواص باور نکردنی هندوانه
شب بیست و سوم ماه رمضان به احتمال قوی شب قدر است
جشنواره ملی رسانه های دیجیتال
درگیری شدید مربی و مدافع آبی پوشان قبل از بازی با سپاهان
نقد فیلم راه رفتن روی سیم
متن و ترجمه اهنگ True Blue از Billie Eilish
8 فایده ی سرکه ی سیب برای سلامتی
فوتبال کره جنوبی و حسرتی 63 ساله!
تست نفوذ پذیری وب سایت اینترنتی
بهترین بازی های اندروید برای سال 2022
تزیین سفره افطار ماه رمضان
روش های بسیار عالی برای تعیین جنسیت فرزند قبل از بارداری
افزایش تمرکز در درس خواندن
مبارزه با تغییرات اقلیمی و مقابله با گرمایش زمین
نرم افزارها و ابزارهای پرداخت
13 عکس متحرک زیبای ساخته شده توسط هنرمند نابینا
اهمیت ورزش کردن برای معلولان
معرفی سالاد شیرازی در مجله نیویورک تایمز؛ طرز تهیه
راز گورستان مخفی – قسمت اول
نبرد قرن ایران و آمریکا پس از 24 سال
7 ویژگی برجسته یک لباس ورزشی مناسب را بشناسید
آشنایی با زندگی و آثار پابلو پیکاسو
شخصیت شناسی با میوه مورد علاقه در شب یلدا
چگونه بدون قلاب دستبند ببافیم ؟
بهترین املاک در منطقه 10 تهران
راهکارهایی ساده برای تسکین علائم بلند مدت کرونای ملایم
بهترین باشگاه های بدنسازی مشهد؛ آدرس و شماره تماس
جاده رؤیایی اسالم به خلخال
اشعار زیبا از پروین اعتصامی
درگاه بانکی واسط چیست و روش های گرفتن آن
عوارض کم خوابی و دیر خوابیدن در کودکان
جام ملت های آفریقا ؛ دیدار رده بندی ؛ تیم ملی نیجریه سوم شد
بیوگرافی عادل غلامی؛ والیبالیست معروف
تصاویر واقعی از آدم فضایی
معرفی و نقد و بررسی فیلم تئوری همه چیز ( استیون هاوکینگ )
خوراک قفقازی با گوشت چرخ کرده
شروع و پایان محرم و صفر 1402
بیوگرافی نجم الدین شریعتی؛ مجری برنامه سمت خدا
چه کارهایی باعث می شود تا روز شادی را شروع کنیم؟
مدیریت اصولی کانال تلگرام
روزهای قمر در عقرب سال ۱۴۰۲
سفید کردن دندان با پوست موز
آشنایی با قلعه مهرجرد در میبد
آماریولدو، ستاره ای که در 23 سالگی طلوع کرد
ده چکاپ پزشکی ساده؛ پیشگیری از بیماریها
بهترین فروشندگان تجهیزات آکوستیک
دلیل استحباب اذان و اقامه
نکاتی کلیدی برای پخت برنج بهتر
اطلاعیه روزنامه رسمی کشور و درج آگهی
دیدارهای خاطره انگیز ; تیمی که در ثانیه 55 بازی، 10 نفره شد
بهترین مارک لوازم آرایشی گیاهی
طرز تهیه آش انار: مخصوص شب یلدا
نقد فیلم جاده قدیم؛ روایت یک تراژدی
عکس های جالب برای کامنت فیس بوک
روشهایی جالب برای جلوگیری از تعریق زیاد
معرفی برند رینوزیت Renuzit
مجموعه کاخهای نیاوران؛ آدرس و ساعات بازدید
اقدامات لازم در زمان مسمومیت غذایی در مسافرت
e-content-wrap” style=”text-align: right;”>
سخنان بزرگان درباره کتاب
ارزش ریال ایران در برابر طلا و دلار
دنیزلی ؛ شهر آب های گرم ترکیه
سریال چرا او؛ بازیگر دختر امپراطور در نقش یک وکیل
تصاویری زیبا و دیدنی از توده های یخی